57210
Let's do something educational now, shall we?
The Laplace operator is a second order differential operator in the n-dimensional Euclidean space, defined as the divergence (∇·) of the gradient (∇ƒ). Thus if ƒ is a twice-differentiable real-valued function, then the Laplacian of ƒ is defined by

Equivalently, the Laplacian of ƒ is the sum of all the unmixed second partial derivatives in the Cartesian coordinates xi:
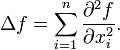
As a second-order differential operator, the Laplace operator maps Ck-functions to Ck−2-functions for k ≥ 2. The expression (1) (or equivalently (2)) defines an operator Δ : Ck(Rn) → Ck−2(Rn), or more generally an operator Δ : Ck(Ω) → Ck−2(Ω) for any open set Ω.
57218
Can you actually do all this?